NMR spectroscopy – 5 interesting facts you should know

Have you guessed any time that molecules can be visualised by scanning their nuclei? Have you thought anytime that all protons are not equal ? All these things come possible with NMR spectroscopy. By reading various protons in the molecule one can guess the structure by using proton NMR spectra. So let’s discuss five interesting things you should know all about this great technique in spectroscopy.

1. What is NMR ?

NMR is the nuclear magnetic resonance spectroscopy where the organic compounds are analysed by the presence of different nuclei in the compound. It is one of the best techniques to determine the structure of compounds by interpreting various peaks in the spectra.

Organic compounds may have various atoms hence different nuclei with either similar or different environment. Let’s take the case of ethane.

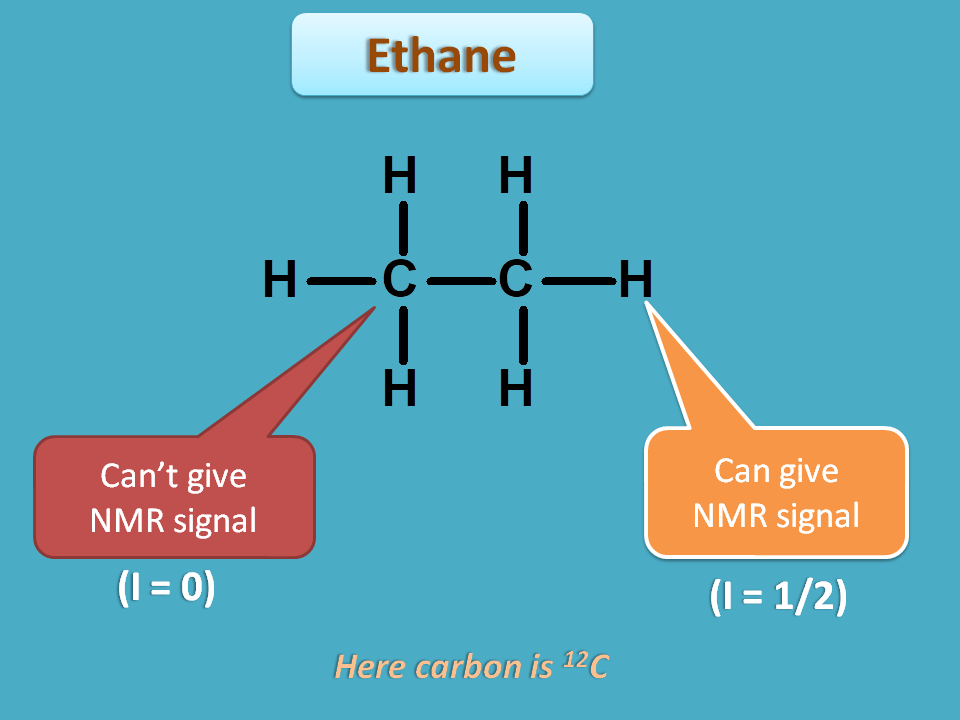
It has two types of nuclei such as carbon and proton. Again it has two carbons and totally six protons.

Every nucleus can’t give NMR signal but those nuclei with spin quantum number I=½ can only give NMR signal. We will see the reason for this in the following discussion.

Suppose a nuclei is under normal state where it has less energy and more stable. If we supply sufficient energy, the nuclei may undergo transition to a new state where it has more energy hence less stable.

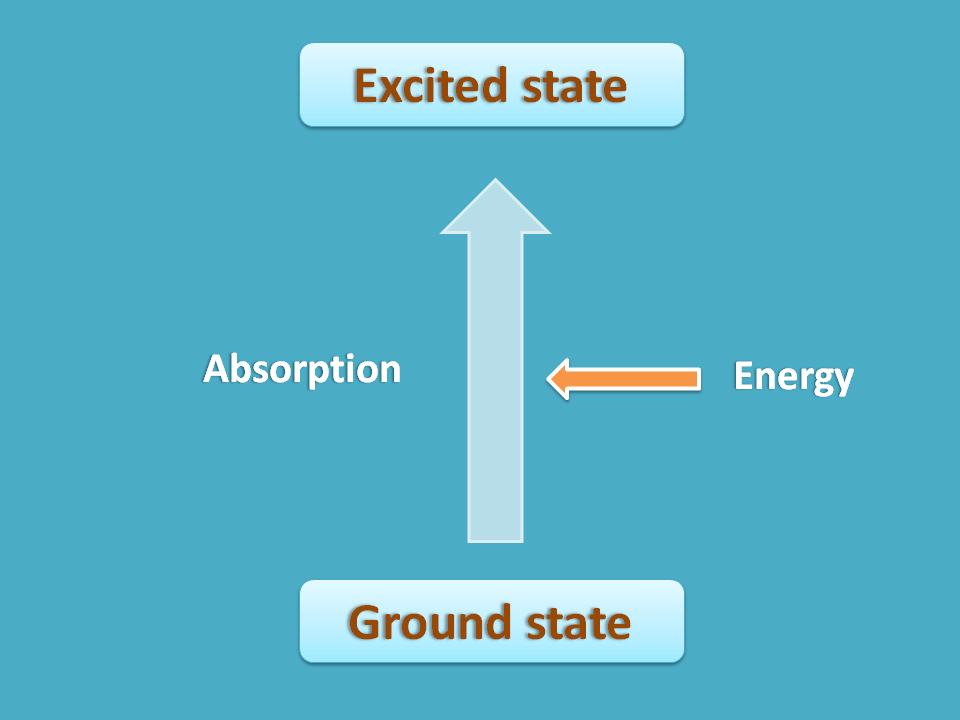
NMR spectroscopy is one type of absorption spectroscopy where the energy is absorbed for nuclear transition. The first state of nuclei where it is more stable can be considered as ground state and second state with less stability as excited state. Now in this process the nuclei in ground state go to the excited state with absorption of energy.

So, a nucleus can have two possible states every time?

Interestingly the answer is “No”. A nucleus always exists in single state under normal conditions but in presence externally applied magnetic field it may have more than one option.

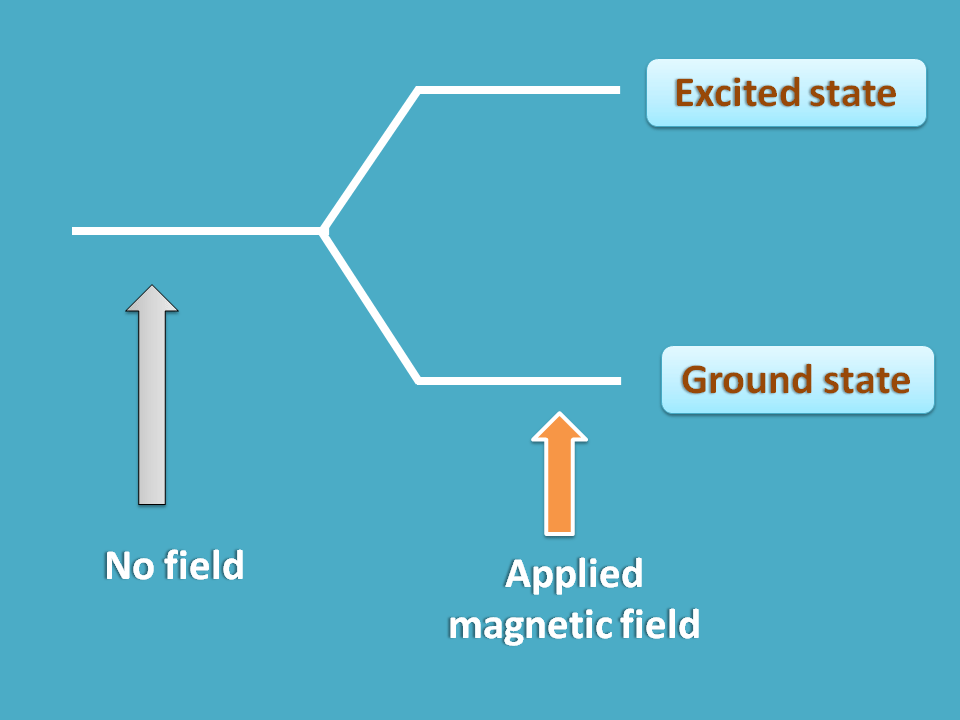
For example, it can align parallel or opposite the applied magnetic field producing two states former with less energy and later with more energy.

So, what we can conclude from the above discussion is that a nucleus should have I=1/2 and should exist in two states such as ground state and excited state to give the signal in NMR spectra.

2. Why I=½ ?

So one of the important question is that why a nucleus should have I=½  and why other type of nuclei can’t give NMR signal?

Yes, as we have seen above, all nuclei don’t fit into the scope of NMR spectra. Let’s take three cases to get more clarification. First we will define magnetic moment number.

 It can be indicated by “m” and

m=2 I+ 1

Now let’s see three cases.

Case 1 : I=0

Here spin quantum number I=0. So,

m=2(0) + 1=1

So the nucleus can exist only in one state even in the applied magnetic field. Also it has I=0 indicating that it has no spin hence can’t absorb energy and not suitable for NMR spectroscopy.

Case 2 : I=½

Now spin quantum number I=½ . Hence

m=2(1/2) + 1=2

Now the nucleus can exist in to states, on with aligning parallel (hence ground state) and with aligning opposite to the applied magnetic field. Such type of nuclei can give NMR signal.

The important nuclei with I=1/2 include

¹H, ¹³C, ¹⁵N, ¹⁹F and ³¹P

Two most popular NMR spectroscopy techniques are 1H NMR and 13C NMR that study ¹H and ¹³C nuclei respectively.

Case 3 : I=1

Now let’s check with I=1.

m=2(1) + 1=3

So the nuclei can exist in three spin orientations such as -1, 0 and +1. Here you can easily observe that all the spin states are not equivalent by magnitude with one state having zero magnitude.

Hence the transitions between these spin states is non-uniform and therefore doesn’t fit well into NMR spectra.

Therefore we can conclude that

3. How NMR spectroscopy works?

Ok, that’s fine, now we know which nuclei can give NMR signal and now we can confirm three requirements for NMR spectra.

• Nuclei with spin quantum number I=½
• Externally applied magnetic filed
• Radiofrequency radiation of sufficient energy

But how it works?

Let’s go in deeper. Here we define three more parameters spin angular momentum, magnetic moment and magnetic energy.

Spin angular momentum

It can defined in terms of spin quantum number and practically it is given by

S=h/2π *(I)

Since I=½,

S=h/2π *(1/2)=h/4π

Magnetic moment

It is the multiple of gyromagnetic ratio with spin angular momentum.

μ=γ * S

Where

γ=gyromagnetic ratio

S=spin angular momentum

Now nuclei with I=½ will have two spin states with different magnetic moment.

μ _+1/2   =γ * (h/4π)=γh/4π

and

μ _+1/2 =γ * (-h/4π)=- γh/4π

Magnetic energy

Now each spinning nucleus in magnetic field will have definite energy which can be obtained by multiplication of magnetic moment with magnetic field strength.

E=μ * B ₀

Where

B ₀ is magnetic field strength

Now, for two spin states

E _-1/2=(-γh/4π) * B ₀  =  -γhB ₀/4π

and

E _+1/2=(+γh/4π) * B ₀  =  +γhB ₀/4π

Now which is ground state? Lower the energy, more the stability. Hence E _-1/2 is the ground state and E _+1/2 is the excited state.

So when we supply sufficient energy in the form of radiofrequency radiation, nuclei in the ground state can be transferred to excited state with absorption of energy.

The energy that should be supplied for this transition hence equals to energy difference between the two states. Therefore

E=E _+1/2 – E _-1/2

  =  (+γhB ₀/4π) – (-γhB ₀/4π)

Hence,

E  =γhB ₀/2π

Since E=hν ,

E=hν=γhB ₀/2π

In another words,

ν=γB ₀/2π

So if we supply this much frequency of radiation we can observe a signal in the NMR spectra. This frequency where nuclei has resonance with applied frequency and therefore undergoes transition is termed as larmor frequency, resonant frequency or precessional frequency with whatever the names used for the same context.

But again you may have one doubt. Molecules may have different nuclei hence different magnetic energy and therefore they resonate at different frequencies. Then how all the nuclei can be detected?

This can be achieved by simply by frequency sweep. The frequency of radiation changes at a constant rate with time and each nucleus, at their specific larmor frequency will be in resonance with applied frequency thereby give NMR signal. In this way peaks of all types of protons can be obtained in proton NMR spectra.

4. How signals are measured?

The next part is how we can measure the signal. The situation in NMR spectroscopy is not so simple as we think. Here we are thinking of nuclei only but what about surrounding electrons?

Yes, electrons surrounding each nucleus are negatively charged and create their own magnetic field which opposes applied magnetic field. This produces a shielding effect on applied magnetic field reducing its effective filed strength on the nucleus under study. So either we have to increase magnetic field strength or decrease radiation frequency to obtain resonance.

Now the net magnetic field (B _net) present on a nucleus is given by

B _net=B _o(1-σ)

where σ is termed as shielding constant or screening constant.

Nuclei are also so smart in that they look like similar but act in different way.

Let’s take an example such as propyl chloride.

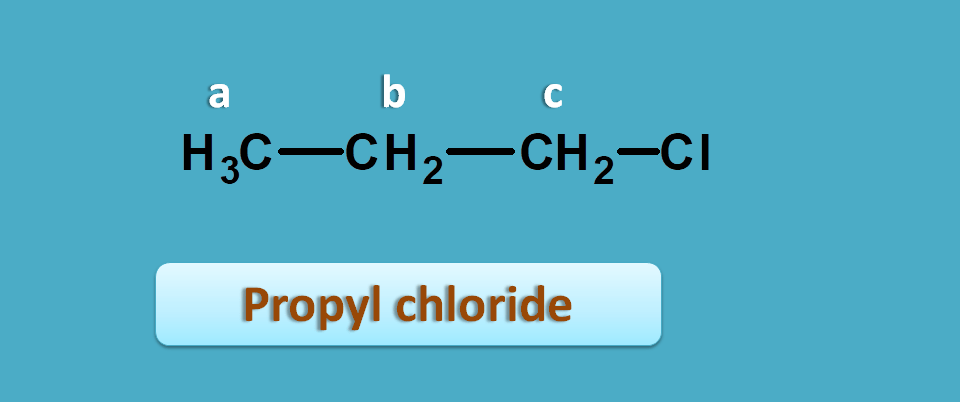
Now here you can observe methyl and methylene protons which are completely different and indicated by “a” and “b” respectively.

What about methylene protons in –CH ₂ and –CH ₂Cl ?

They are also different. Even they look similar their environment is different. Presence of chlorine in –CH ₂Cl makes a different environment.

So these protons have different shielding effects with protons in –CH ₂Cl being less shielded due to electro negativity of chlorine which pulls electron away from protons.

Since shielding constant varies with electron density surrounding a nucleus, it is difficult to exactly measure where the signal appears in NMR spectra and what it is.

To solve this complexity, a standard was selected in NMR spectroscopy which has the highest shielding effect and the signals of protons are measured as relative distance from this peak.

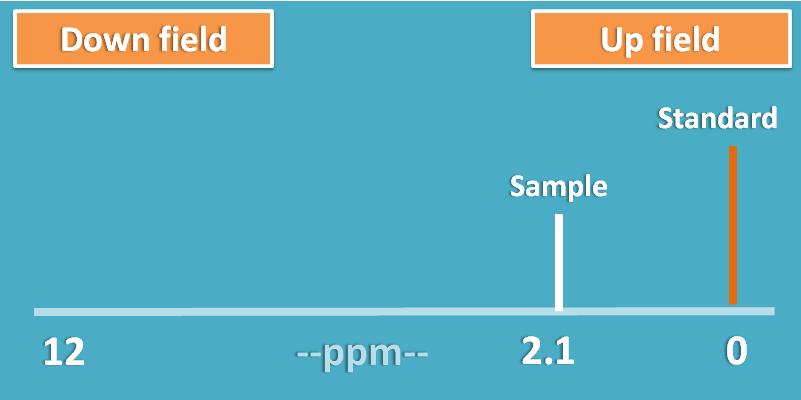
This shift of the peak is measured in terms of parts per million (ppm) and termed as chemical shift.

If a proton is more shielded it will fall nearer to standard peak decreasing chemical shift.

5. How it is used?

Now we come to last and of course main part of our discussion. What is the use of NMR spectroscopy?

It is one of the best tools to determine the structure of unknown compounds. If you have molecular formula of the compound in your hand you can carefully interpret the NMR spectra and predict which type of nuclei may present in the compound.

Number of peaks

Let’s have simple illustration with two structures. Suppose you have two samples of ethanol and propanol. You don’t know which sample contains ethanol. You can use proton NMR spectra to detect the samples.

Ethanol has three different protons labelled by letters a, b and c. This compound cna be indicated by NMR notation as A₃B₂C₁ each alphabet indicated a different type of proton with their relative number as the subscript. So we can easily conclude that ethanol gives three NMR signals.

On the other hand, propanol has 4 different protons. The methylene protons indicated by “b” are different from those indicated by “c”. Hence it gives four signals.

So the sample producing three NMR signals is ethanol.

To learn more about number of peaks for a sample, see

• How to determine the number of peaks in proton NMR.

It is an astonishing fact that this wonderful tool, NMR spectroscopy, is used to determine the structure of compounds just by studying a little nuclei, simply that is proton. Now a small doubt may peep into your mind on practical feasibility of NMR spectroscopy.

Yes, that's about the solvent. Which type of solvent should be selected? is that solvent contains protons and interferes with study?

Really, it is a point to consider. As we are studying protons in the analyte, the protons of solvent used in NMR will definitely interfere with study. Therefore a solvent without any protons should be selected. This can be achieved by deuterated solvents where all protons are replaced by deuterium.

Integral ratio

Sometimes, we can also predict compounds based on the integral ratio.

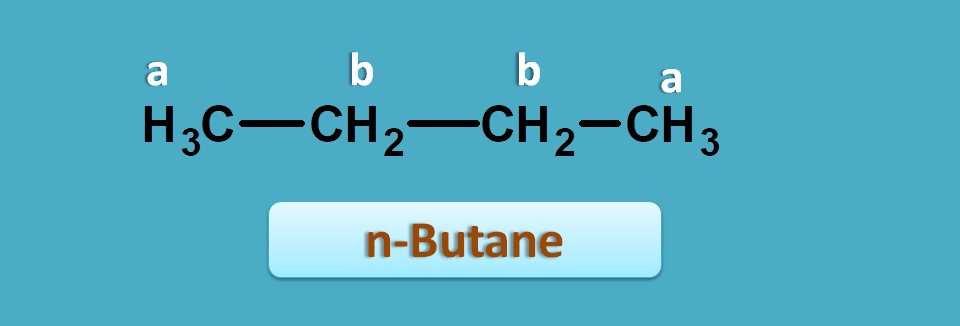
Let’s have an example. Again we have two samples each contain a butane isomer. These isomers can be detected by NMR spectroscopy.

Butane can exist as two isomers such as n-butane and iso-butane. Now if you predict NMR spectra for the first structure, it has two types of protons indicated by a and b. Here you can find totally six methyl protons indicated by letter 'a' which are both chemically and magentically equivalent. Similalry four methylene protons indictaed by letter 'b' are again equivalent. Hence it gives 2 NMR signals.

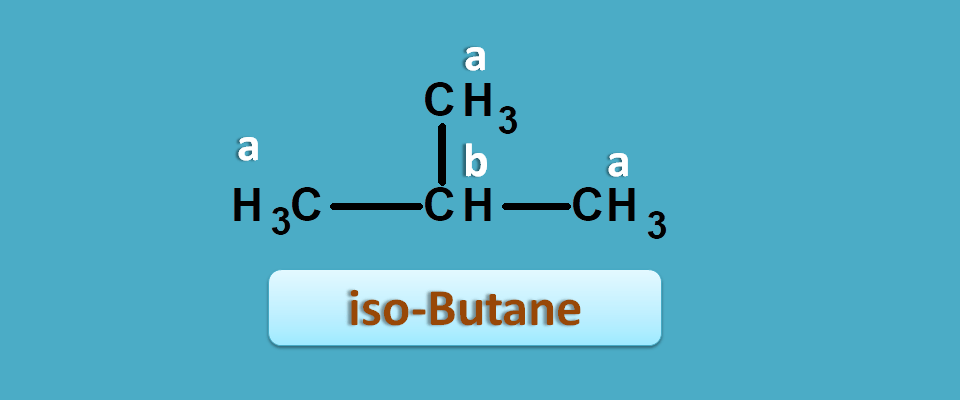
Similarly iso-butane again has two different protons hence give 2 NMR signals.

But the integral ratio of both samples will be different and it can be defined as the relative ratio of area under peak of two signals

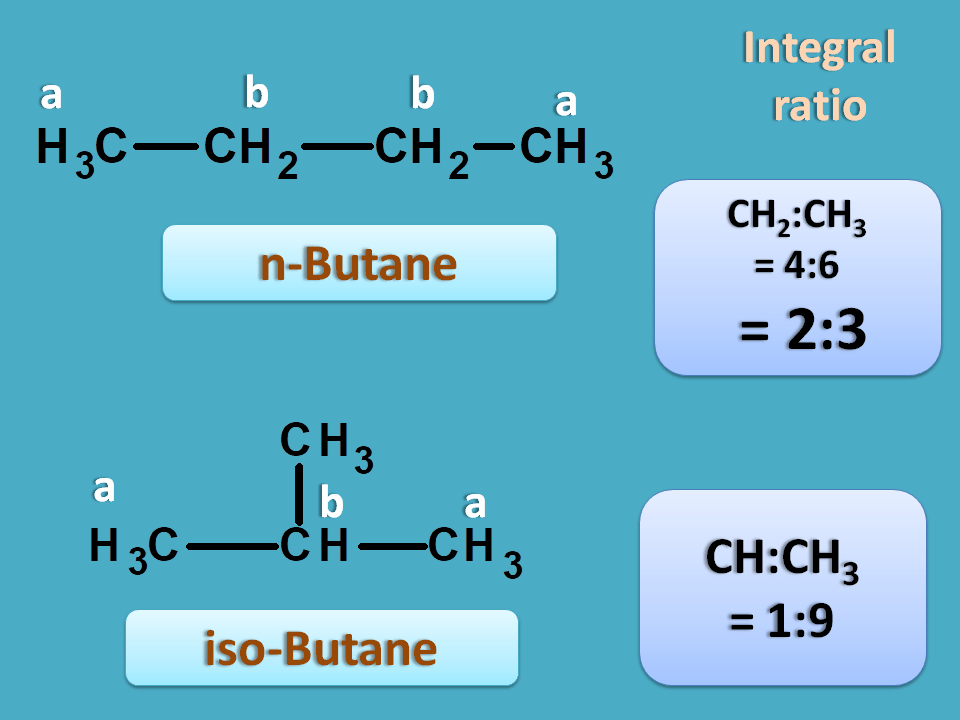
Fortunately, we can predict it even from structure for simple compounds. Integral ratio is equal to the ratio of the total number of equivalent protons corresponding to each peak.

So in n-butane,

Total number of methyl protons=6

Total number of methylene protons=4

Hence integral ratio=4 : 6=2:3

Similarly in iso-butane,

Total number of methyl protons=9

Total number of methylene protons=1

Hence integral ratio=1 : 9

So the sample producing an integral ratio of 1:9 is isobutane and 2:3 is n-butane.

Chemical shift

We can also use chemical shift to assign peaks to the specific part of the structure. Let’s take 2-butanone as an example.

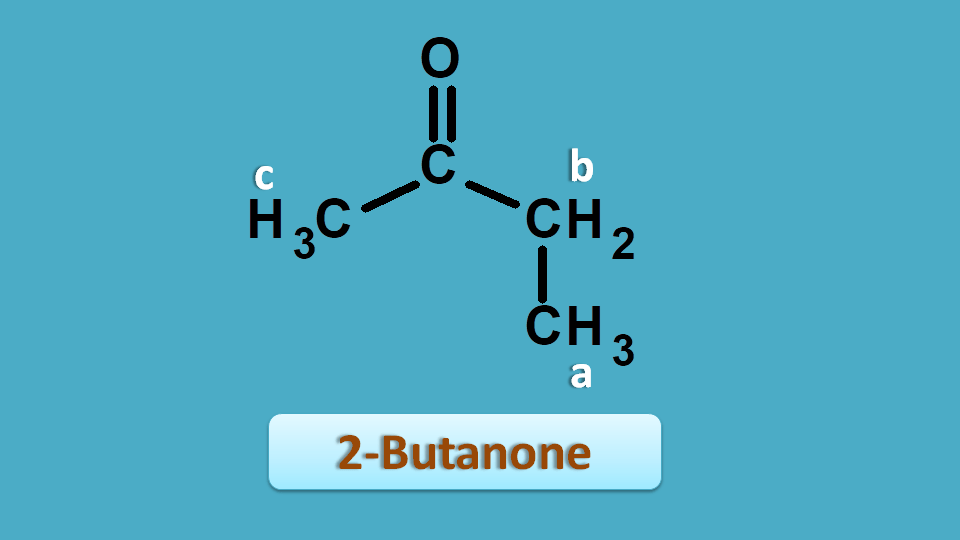
From the above discussion you can clearly observe that all the protons are non-equivalent hence give different signals. So it has shown 3 peaks at 2.5, 2.1 and 1.0 ppm.

But how to assign peak for a particular proton?

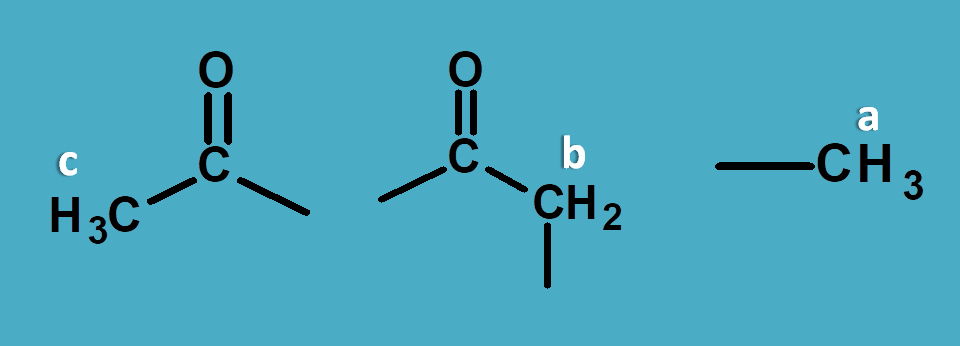
This can be achieved by reading approximate values from NMR spectrum table . According to this table saturated alkyl proton fall in the region of 0 to 1.5 and allylic, α-keto protons fall in the region of 1.5 to 2.5 ppm.

Again approximate values for methyl and methylene protons are 0.9 and 1.3 ppm respectively.

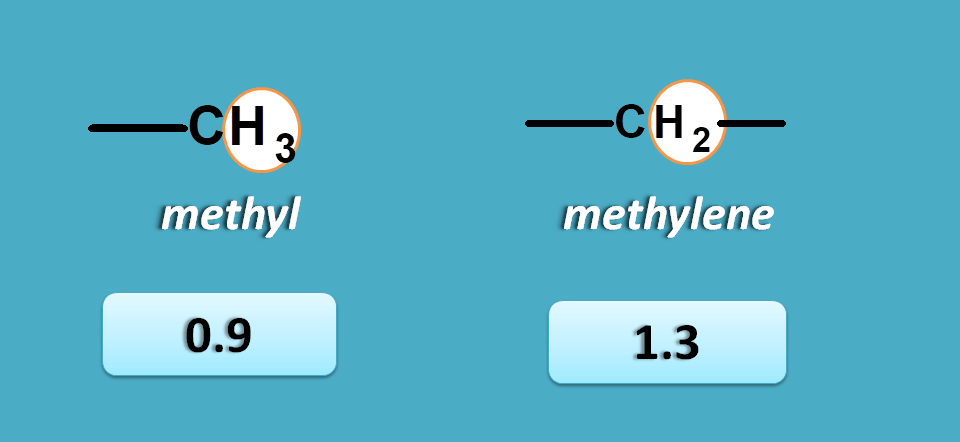
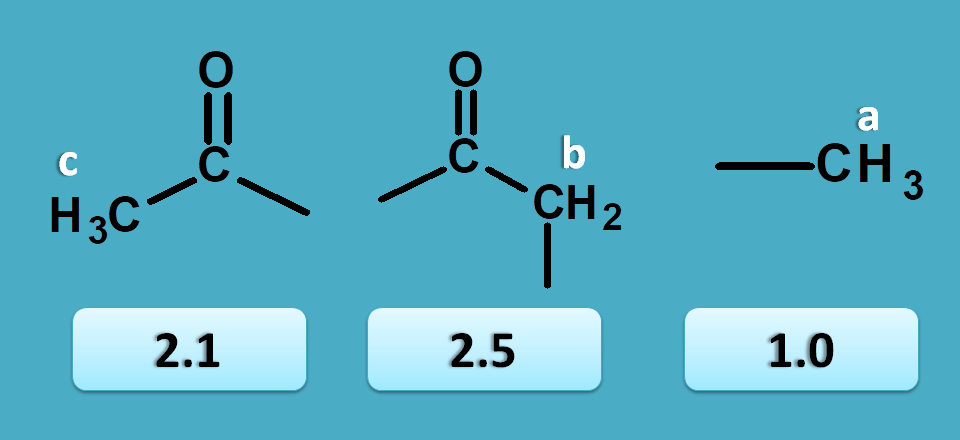
So here peak corresponding to 1.0 ppm is due to methyl protons.

Now other peaks 2.1 and 2.5 are due to α-keto protons. As methyl protons will have less chemical shift than methylene protons, 2.1 corresponds to CH ₃-C=O- and 2.5 corresponds to –(C=O)-CH ₂– .

In this way we can predict the structure of organic compounds by using NMR. Even it can also be used for study of configuration and conformation of organic compounds.

So that’s about all interesting facts about NMR spectroscopy. It is a great tool in the chemical analysis providing key details of structure for many organic compounds. Please share this post if you like.